Solar land area
Download Jupyter Notebook File: ipynb File
How many times have you heard the claim that "we can power the world with solar photovoltaic (PV) power". After encountering many false claims, I will now subject it to thorough engineering analysis. I will outline the critical assumptions needed to estimate the land area that solar farms would need to cover including un-panelled site-access area.
Several methodologies exist for estimating the land area capacity of solar power. I will utilize 'Average Practical PV Output' data, which is available country by country in terms of kWh/kWp/day. I.e. average energy output to grid per unit of capacity per day. This method, widely employed and supported by renewable energy advocates, conveniently provides a modest accounting for several confounding factors associated with solar energy production including panel efficiency, self-shading and soiling.
This study does not account for all the auxiliary areas associated with solar farms. These areas include extensive mining and manufacturing facilities necessary for the production and maintenance of solar panels.
The analysis adopts a 'copper-plate model'. This modeling approach overlooks the infrastructure and limitations of energy transport, assuming, simplistically, that all system components are situated in one place.
Land area calculations for solar capacity are based on preliminary site selection. However, as securing ideal sites becomes more challenging, later sites will likely be less optimal. Consequently, this study does not take into account the self-shading effect of the undulating terrain itself, or other siting limitations that can affect the efficiency of solar energy production.
This analysis does not consider the potential role of thermal solar power, which has the potential to outperform PV technology in providing efficient, low-grade water-heating solutions.
Primary energy consumption data is relatively consistent across sources such as BP, EIA, and IEA. For this analysis, I will use data from BP, the most frequently cited source for primary energy information.
Capacity Factor Data¶
The capacity factor is the actual output of the panels divided by the maximum output potential of the panels for a whole year. This is obviously better in sunny countries and worse in less-sunlit countries. The capacity factor also changes dramatically between winter and summer in countries which are far from the equator, so here we are looking at a year-average.
The capacity factor for each country can be obtained from the Global Photovoltaic Power Potential by Country dataset. This data, is compiled by Solargis and was funded by the World Bank.
This data operates under the assumption of freestanding structures utilizing monofacial crystalline silicon PV modules, which are mounted at an optimal tilt to maximize annual energy yield. It also considers the use of high-efficiency inverters.
The data factors in solar radiation, air temperature, and terrain to simulate the energy conversion and losses in the PV modules and other components of a PV power plant. It presumes a 3.5% loss due to dirt and soiling, while the aggregate impact of other conversion losses—including inter-row shading, mismatch, inverters, cables, and transformers—is estimated at 7.5%. The power plant availability is assumed to be 100%.
The key column we need, labeled 'Average practical potential kWh/kWp/day' in the source data essentially represents the year-averaged capacity factor multiplied by 24. Refer to footnote for more details.
| Capacity Factor [%] | |
|---|---|
| Country | |
| Namibia | 22 |
| Chile | 22 |
| Jordan | 22 |
| Arab Republic of Egypt | 22 |
| Republic of Yemen | 22 |
| ... | ... |
| Estonia | 12 |
| Isle of Man (U.K.) | 12 |
| Norway | 12 |
| United Kingdom | 11 |
| Ireland | 10 |
207 rows × 1 columns
Some of the least sunlit regions correspond to the most developed countries worldwide, a fact that may surprise many. Equally surprising is that the sunniest regions only possess double the capacity factor of the least sunny ones. However, the capacity factor isn't the only determinant of potential solar energy utilization.
A significant challenge confronting these northern countries is the temporal disparity of solar energy availability. The majority of solar energy is received during long summer days, and currently, there are no efficient methods to store such large quantities of electricity for an extended period of six months.
The average global capacity factor, when accounting for land area, is as follows:
Solar Potential Assumptions¶
We can now begin to formulate a reasonable estimate for the net amount of electricity solar power can deliver, taking all lifetime costs into account. Essentially, we're seeking to determine the average annual solar power output per unit of land area, expressed in electrical energy output, per second, per square metre. This is expressed in the unit of "watts" per square meter (W·m⁻²).
The most crucial factor is the installed capacity of existing solar farms. It may seem intuitive to calculate solar PV potential simply by multiplying the incident radiation energy by the panel's efficiency. However, this approach overlooks several important aspects.
We must also account for factors like construction, maintenance, disposal, recycling, and transportation, which are currently supported by the existing fossil fuel infrastructure. These elements play a significant role in the comprehensive understanding and evaluation of solar power potential.
| Symbol | Name | Description | Source |
|---|---|---|---|
| C_f | Capacity Factor | Average output divided by installed capacity (from SolarGIS paid for by World Bank) | known per country |
| C | Installed Capacity [W/m^2] | Installed capacity (max possible output) of solar power per unit land area in Watts / square metre | assumption |
| E | Embodied Energy | Total lifetime output minus that used to construct and maintain the panel as a proportion of lifetime output | assumption |
| A | Availability | The proportion of time that the plant is available to generate power | nan |
As a first start, lets take the following optimistic estimates and apply them to the global totals to get a minimum estimate of the global land area we will need to cover with solar farms.
Installed Capacity of Farms
What is call the installed capacity is often called the 'capacity density', 'land-use efficiency' or LUE in the literature.
The installed capacity per unit area depends on what sort of panel efficiency and layout density the solar farm can achieve. The relevant value is the “MW-ac” – the alternating current that it is capable of sending to the Grid after electrical inversion. This is approximately 80% of the “MW-dc”. Hereafter, I refer to MW-ac simply as MW.
- California Solar PV Land Use efficiency in 2013 was 35W/m2.
- The US Average Land Use efficiency in 2013 was 42.5 W/m2 (5.8 acres/MW) for a Fixed Axis, Large (>20MW) capacity-weighted average.
- https://www.cell.com/cms/10.1016/j.joule.2021.03.005/attachment/c2b79392-88f9-4231-833d-faf1a0a2a125/mmc1
Embodied Energy
It typically takes the first 2 years of the solar panel's 20 year life to pay back the embodied energy consumed in the manufacturing. We have to account for this by discounting at least 10% of the lifetime energy output. The first two years are the most productive part of the panel life, but lets assume energy output doesn't decay through the lifetime. Some energy is also required for cleaning, repair, recycling, transport and disposal.
Availability Factor
In a solar PV power plant, the plant availability factor is one of the important factors to be evaluated. This depends on the operative functioning of various components and grid regulation. This paper looked at a single industrial scale plant over 5 years, and found an average of 95%. From the analysis, it is observed that tripping time greatly effects the availability factor of inverter as well as the PV plant.
Needless to say, these estimates are unrealistic, especially the overbuild factor. But they provide a bare minimum unachievable according to the laws of physics.
Now I will use these scaling factors to calculate the total area of solar panels required.
Therefore solar can produce:
Total Power Consumption¶
Primary Energy consumption data¶
BP Statistical Review of World Energy is the most widely trusted and canonical estimate of primary energy consumption used worldwide.
The definition of Primary energy is the total chemical energy in the fossil fuels burned that year, plus the the equivalent amount of fossil fuel input required to generate electricity produced by non-fossil sources in a fossil fuel power plant assuming 40.625% efficiency. See footnotes
BP only lists the consumption of the 81 main countries. Other countries are categories in to groups such as "Other Caribbean".
I immediately convert the data "primary_ej" into annual averaged Watts.
| Primary Energy Consumption [GW] | |
|---|---|
| Country | |
| Total World | 18870 |
| Total Non-OECD | 11581 |
| Total Asia Pacific | 8638 |
| Total OECD | 7289 |
| China | 4998 |
| ... | ... |
| Other Southern Africa | 6 |
| Latvia | 5 |
| Luxembourg | 5 |
| Cyprus | 3 |
| North Macedonia | 3 |
104 rows × 1 columns
But now, we need to make a few assumptions in order to use these values to calculate land area. This is where the common-sense comes in.
Energy Demand Assumptions¶
The first step is to scale the primary energy down according to some assumptions to get the actual energy demand we are intending to supply
| Symbol | Name | Description | Source |
|---|---|---|---|
| P | Primary Energy [W] | Average consumption in Watts averaged over most recent year: 2021 (from BP) | known per country |
| G | Growth in Consumption | Factor by which the primary energy consumption has grown when this plan is implemented | assumption |
| S | Solar Proportion | Fraction of energy that solar will supply | assumption |
| R | Efficiency Factor | Factor by which electrifying transport and heating and changing behavior can reduce final energy demand | assumption |
| D | Electricity Correction | Factor by which to correct the total amount of primary energy ignoring waste heat from non-fossil fuels when producing electricity | nan |
| O | Overbuild | Factor of overproduction required to account for insufficient storage for intermittent supply | assumption |
Electrical Demand Correction
Note that these primary energy figures from BP (and IEA and EIA) were originally designed to measure fossil fuel consumption not the useful energy that they provide accounting for conversion efficiency. Obviously, the primary energy used in generating electricity is much higher than the electricity provided as most of the chemical energy of the fuel is lost as waste heat, out of the cooling towers. So when it comes to non-fossil generated electricity, to make for a useful comparison, they convert the electricity generated by non-fossil fuels, in terms of the fossil fuel energy that would have been required to produce the was generated using a conversion efficiency of 40.625%.
In other words the electrical component of this of this fossil fuel demand is only 40% of the primary energy figures in the BP data. About 1/3 of primary energy is used to generate electricity. Therefore, nuclear and renewables only need to replace 1/3 * 0.4 + 2/3 = 80% of primary energy supply to meet demand.
Proportion of Solar¶
Lets assume that solar supplies all our power as many people smart people seem to believe. For example Elon Musk is very bullish on the potential of solar. At an on-stage conference appearance, he says “you could easily power all of China with solar”, to rapturous applause. Twitter is often swayed by infographics claiming the same. For example: an area of panels the size of Spain accompanied by the claim, that it could power the world. Elon replied with: ‘Exactly’. Elon Musk used a graphic in his Tesla Power Wall presentation in 2015 in which he showed a tiny blue square, the size of Connecticut intended to represent the area of solar panels to power the entire USA.
This excellent video claims that the area required to power all of the world is close to the size of france (551,695 square km),
Growth in Consumption
Lets make the unrealistic assumption that growth remains constant despite the certainty that it will rise. The OECD countries (Europe, North America, Australia and East Asia) represent around half the world's energy consumption despite possessing less than 1/5 of the population. But the developing world is catching up fast. For the Non-OECD to just to reach the standard of OECD, we will have to triple global energy consumption. Lets assume, miraculously, that it remains constant.
Electrical Efficiency Factor
Electrifying heating and transport can make things more efficient. It important to distinguish this from the fact that most of the fossil fuel energy used to generate electricity is waste heat which we don't need to provide at all - we've already accounted for this;
I delved into the electrification efficiency question separately. In summary, according to the most optimistic observers, we can hope to save 40% from:
- The higher energy-to-work conversion efficiency of using electricity for heating, heat pumps, and electric motors, and using electrolytic hydrogen in hydrogen fuel cells for transportation, compared with using fossil fuels (Table S4);
- The elimination of energy needed to mine, transport, and refine coal, oil, gas, biofuels, bioenergy, and uranium;
- Assumed modest additional policy-driven energy-efficiency measures beyond those under BAU.
These factors decrease average demand ∼23.0%, 12.6%, and 6.9%, respectively, for a total of 42.5%. Thus, WWS not only replaces fossil-fuel electricity directly but is also an energy-efficiency measure, reducing demand.
The mental gymnastics involved in getting to this number are great. Notably, the figure of 40% savings ignores the fact that electrifying end-use demand incurs a cost of 4-15% of grid-losses. There are other biases which interfere with this estimate. Therefore, I will estimate 20% savings.
Overbuild Factor
Capacity credit, is how much of nameplate capacity can counted on as to reliably serve load at peak demand. Solar without storage has a capacity value of 0 when the peak demand is close to sunset, which it normally is, which makes solar functionally useless without storage.
The key problem is storage. The terms "primary," "secondary," and "tertiary" are often used to refer to different types of reserve or response services. These are services that actually exist:
- Primary Reserve/Response on a second to second basis is regualted by spinning reserves from traditional power plants (i.e., additional capacity from generators that are already connected to the system and spinning but not producing power)
- Secondary Reserve/Response: within 30 seconds, automatic increase in generation (or reduction of demand) when the frequency is below 50Hz.
- Tertiary typically involves bringing new plants online, within an hour or so.
But no country has (with the exception of high-hydro penetration countries such as Norway and Brazil) have enough storage to make it through a single night. I have done calculations for nightly electricity storage requirements. These are unfeasible in terms of cost (4000x global GDP) for the lithium, lithium reserves (24x times speculated reserves) and lithium production rate (17,000 years to mine the sufficient lithium). We can forget about inter-day storage.
Beyond this is seasonal storage. We need seasonal storage in order to not freeze to death in the winter. The United States for example consumes 52% of its primary energy during the colder half of the year (October to March), but the solar output the US in this period is only 44% of the total.
This is a big issue because earlier, we assumed we were only going to build enough solar panels so that our solar energy production matched the energy consumption over the course of the whole year, not each month.
At least 6% (1763TWh) of annual energy demand would need to be stored from the summer to be used over the winter (again using Jacobson's optimistic 42.5% electrical efficiency factor). The brand-new battery storage facility in Escondido, California, has a capacity of 120MWh and uses 0.00486km2. We would need 14.7 million of these. In terms of land area this is 267x267km, 71,400km2, 0.9% of US lower 48, the size of Ireland.
The obvious solution is to this is to increase the solar capacity so that seasonal storage isn't required. The most adverse month December, with a capacity factor of 13% and a supply shortfall 667TWh of solar electricity. Covering this requires the addition of 25000km2, 158x158km of solar farmed land.
In fact, because of the difficulty of storing electrical energy, most sane plans actually propose an overbuild capacity of 5 to 15 times the annual demand. This is to account for the low capacity value of solar. Capacity value is how much of nameplate capacity can counted on as to reliably serve load at peak demand. For solar, this value is 0% during the colder half of the year because peak demand occurs during darkness.
A factor of 5 overbuild for capacity is 840000km2, 917x917km. This is the minimum extent of solar farms required to reduce energy storage to an overnight problem. Not much more can be said here.
Thus, we end up with the final energy demand of:
Area of Land Required¶
To get the land area required, we just divide the energy consumption by energy production intensity of the land.
It seems like a lot. But what does it mean in terms of the space we have left on planet earth?
Therefore a minimum of around a percent of the earth's land area is required to sustain our present energy needs.
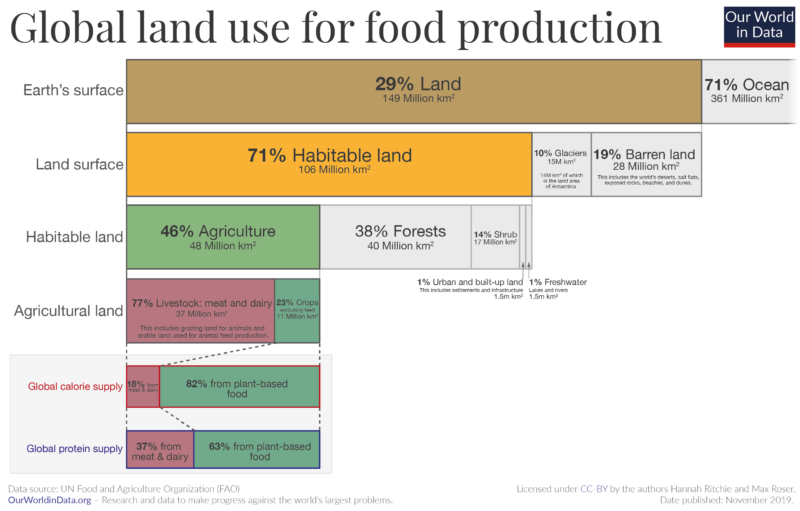
Land is primarily used for agriculture. Note how on this diagram, only 1% is 'Urban area and built up land'. Its true that a huge quantity of land is managed for farming. But it is one thing tending to crops and another thing building physical infrastructure.
A study of global inventory of the spatial distribution and density of roads, parking lots, buildings, driveways, sidewalks and other manmade surfaces, which it called 'constructed impervious surface area (ISA)' was published in 2007 by a collaborative team involving US National Geophysical Data Center, NASA and US Department of Energy. It measured the reflectivity of the ground using satellite imagery. The global ISA represents the extant footprint of every structure human civilisation has created. It estimated the ISA to be 579,703 km². An area the size of France.
The solar area is technically the land-use for the entire farm, of which around half to a third depending on access requirements and the need for spacing to overcome self-shading. So the necessary panel area is at a minimum, several times larger than that of existing human structures.
The point here is that when we are looking at the feasibility of installing physical infrastructure such as solar panels, the relevant point of comparison it is land occupied by other physical structures. Agricultural land, wild land or forest land is incomparable. So, this typical article from 'nextenergysolar' spends thousands of words failing to mention the relevant point.
Lets calculate the area required for all nations using the same parameters:
| Land Required by Solar Farms [%] | |
|---|---|
| Country | |
| Singapore | 9390.3 |
| Hong Kong | 1743.5 |
| Netherlands | 246.2 |
| Korea, Republic of | 231.2 |
| Qatar | 230.9 |
| ... | ... |
| Kazakhstan | 2.0 |
| Argentina | 1.9 |
| Algeria | 1.4 |
| Peru | 1.3 |
| Australia | 1.1 |
76 rows × 1 columns
It actually doesn't look so bad for many of the less densely populated, sunnier countries. The problem is in europe in particular, the place that seems most interested by solar power. See fullscreen here
Primary Energy¶
BP is the source for present and historic consumption used by Our World in Data.
Gap-Minder still quotes the World Bank estimates of primary energy even though this is no-longer available.
The definition of Primary energy is the:
- total chemical energy in the fossil fuels burned that year,
- plus the the equivalent amount of fossil fuel input required
to generate electricity produced by non-fossil sources in a fossil fuel power plant assuming 40.625% efficiency.
- plus an estimate of the biomass chemical energy burned from the supply of electricity using biomass assuming 32% efficiency.
Traditionally, in bp’s Statistical Review of World Energy, the primary energy of non-fossil based electricity (nuclear, hydro, wind, solar, geothermal, biomass in power and other renewables sources) has been calculated on an ‘input-equivalent’ basis – i.e. based on the equivalent amount of fossil fuel input required to generate that amount of electricity in a standard thermal power plant.
For non-fossil electricity (excluding biomass-powered electricity)
2018 onwards: the annual rate of efficiency improvement is based on the simplified assumption that efficiency will increase linearly [from 40%] to 45% by 2050. [I.e. it is assumed as 40.625% in 2022]
For Bio-mass plants:
In this edition, we assume a constant efficiency of 32% for biomass power to better reflect the actual efficiency of biomass power plants.